Same maximum figure of merit ZT(=1), due to the effect of impurity size, obtained in the n(p)-type degenerate InAs-crystal 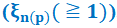 , at same reduced Fermi energy
, at same reduced Fermi energy 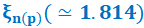 , same minimum Seebeck coefficient
, same minimum Seebeck coefficient  , and same
, and same 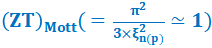
DOI: 10.54647/physics140567 90 Downloads 14076 Views
Author(s)
Abstract
In our two previous papers [1, 2], referred to as I and II. In I, our new expression for the extrinsic static dielectric constant, \varepsilon\left(r_{d\left(a\right)}\right), r_{d\left(a\right)} being the donor (acceptor) d(a)-radius, was determined by using an effective Bohr model, suggesting that, for an increasing r_{d\left(a\right)}, \varepsilon\left(r_{d\left(a\right)}\right), due to such the impurity size effect, decreases, and affecting strongly the critical impurity density in the metal-insulator transition and also various majority carrier transport coefficients given in the n(p)-type degenerate InAs -crystal, defined for the reduced Fermi energy \mathbf{\xi}_{\mathbf{n}(\mathbf{p})}(\geqq\mathbf{1}). Then, using the same physical model and same mathematical methods and taking into account the corrected values of energy-band-structure parameters, all the numerical results, obtained in II, are now revised and performed, giving rise to some important concluding remarks as follows.(1) The critical donor (acceptor)-density, N_{CDn\left(NDp\right)}(r_{d(a)}), determined in Eq. (3), can be explained by the densities of electrons (holes) localized in exponential conduction (valance)-band (EBT) tails, N_{CDn\left(CDp\right)}^{EBT}(r_{d(a)}), given in Eq. (21). (2) In Tables 9-10, with a given d(a)-density N [=2\timesN_{CDn\left(NDp\right)}(r_{d(a)})], one notes here that with increasing temperature T(K): (i) for reduced Fermi energy \xi_{n(p)}(\simeq1.814), while the numerical results of the Seebeck coefficient S present a same minimum \left(=-1.563\times{10}^{-4}\frac{V}{K}\right), those of the figure of merit ZT show a same maximum ZT\left(=\mathbf{1}\right), (ii) for \xi_{n(p)}=1, those of S and ZT present same results: Sb\left(=-1.322\times{10}^{-4}\frac{V}{K}\right) and 0.715, respectively, (iii) for \xi_{n(p)}\simeq1.814 and \xi_{n(p)}=1, the same values of the well-known Mott figure of merit, \left(ZT\right)_{Mott}=\frac{\pi^2}{3\times\xi_{n(p)}^2}(\simeq1 and 3.29), are respectively investigated, and finally, (iv) we show here that in the degenerate InAs-semiconductor, the Wiedemann-Frank law, given in Eq. (25a), is found to be exact.
Keywords
Effects of the impurity-size and heavy doping; effective autocorrelation function for potential fluctuations; optical, electrical, and thermoelectric properties; figure of merit; Wiedemann-Franz law
Cite this paper
H. Van Cong,
Same maximum figure of merit ZT(=1), due to the effect of impurity size, obtained in the n(p)-type degenerate InAs-crystal 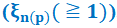 , at same reduced Fermi energy
, at same reduced Fermi energy 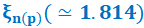 , same minimum Seebeck coefficient
, same minimum Seebeck coefficient  , and same
, and same 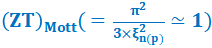 , SCIREA Journal of Physics.
Volume 8, Issue 4, August 2023 | PP. 431-455.
10.54647/physics140567
, SCIREA Journal of Physics.
Volume 8, Issue 4, August 2023 | PP. 431-455.
10.54647/physics140567
References
| [ 1 ] | H. Van Cong, “New dielectric constant, due to the impurity size effect, and determined by an effective Bohr model, affecting strongly the Mott criterion in the metal-insulator transition and the optical band gap in degenerate (Si, GaAs, InP)-semiconductors, “SCIREA J. Phys., vol.7, pp. 221-234 (2022); H. Van Cong et al., “Size effect on different impurity levels in semiconductors,” Solid State Communications, vol. 49, pp. 697-699(1984); H. Van Cong, “Accurate expressions for optical coefficients, given in n(p)-type heavily doped InSb-crystals, due to the impurity-size effect, and obtained from an improved Forouhi-Bloomer parameterization model,” SCIREA J. Phys., vol.8, pp. 280-305 (2023); H. Van Cong, “Accurate expression for optical coefficients, given in n(p)-type heavily (lightly) doped InAs-crystals at any temperature T, due to the impurity-size effect, and obtained from an improved Forouhi-Bloomer parameterization model (FB-PM),” SCIREA J. Phys., vol.8, pp. 306-331 (2023). |
| [ 2 ] | H. Van Cong, “Effects of donor size and heavy doping on optical, electrical and thermoelectric properties of various degenerate donor-silicon systems at low temperatures,” American Journal of Modern Physics, vol. 7, pp. 136-165 (2018). |
| [ 3 ] | H. Van Cong et al., “A simple accurate expression of the reduced Fermi energy for any reduced carrier density. J. Appl. Phys., vol. 73, pp. 1545-15463, 1993; H. Van Cong and B. Doan Khanh, “Simple accurate general expression of the Fermi-Dirac integral and for j> -1,” Solid-State Electron., vol. 35, pp. 949-951(1992); H. Van Cong, “New series representation of Fermi-Dirac integral for arbitrary j> -1, and its effect on for integer j,” Solid-State Electron., vol. 34, pp. 489-492 (1991). |
| [ 4 ] | C. Kittel, “Introduction to Solid State Physics, pp. 84-100. Wiley, New York (1976). |
| [ 5 ] | S. Adachi, “Physical Properties of III-V Semiconductor Compounds,” John Wiley & Sons, Inc., New York, 1992. |
| [ 6 ] | H. Van Cong et al., “Optical bandgap in various impurity-Si systems from the metal-insulator transition study,” Physica B, vol. 436, pp. 130-139, 2014; H. Stupp et al., Phys. Rev. Lett., vol. 71, p. 2634 (1993); P. Dai et al., Phys. Rev. B, vol. 45, p. 3984 (1992). |
| [ 7 ] | H. Van Cong, K. C. Ho-Huynh Thi, et al., “28.68% (29.87%)- Limiting Highest Efficiencies obtained in Crystalline Silicon Junction Solar Cells at 300K, Due to the Effects of Heavy (Low) Doping and Impurity Size, “SCIREA J. Phys., vol.7, pp. 160-179, 2022; H. Van Cong, K. C. Ho-Huynh Thi, et al., “30.76% (42.73%)-Limiting Highest Efficiencies obtained in Crystalline GaAs Junction Solar Cells at 300K, Due to the Effects of Heavy (Low) Doping and Impurity Size, “SCIREA J. Phys., vo.7, pp. 180-199 (2022). |
| [ 8 ] | J. Wagner and J. A. del Alamo, J. Appl. Phys., vol. 63, 425-429 (1988). |
| [ 9 ] | P. W. Chapman, O. N. Tufte, J. D. Zook, and D. Long, Phys. Rev. 34, 3291-3295 (1963). |
| [ 10 ] | M. Finetti and A. M. Mazzone, J. Appl. Phys. 48, 4597-4600 (1977). |
| [ 11 ] | Hyun-Sik Kim et al.,”Characterization of Lorenz number with Seebeck coefficient measurement”, APL Materials 3, 041506 (2015). |

